Physical Meaning of the term Derivative
Instantaneous rate of change of function w.r.t independent variable. limit (Δy/Δx) Δx→0
Geometrical Meaning of the term Derivative
It gives the slope of the tangent drawn to the curve at x=a.
Tangent- It is the limiting case of the secant slope of the secant.

Slope of Secant AB- mAB = f(a+h) – f(a) ⁄ (a + h – a)
f ’ (a+) = lim (h→0) f(a+h) – f(a) / h = slope of tangent at A from RHS
f ’ (a+) = Right hand derivative at x=a
mAB’ = f(a-h) – f(a) ⁄ (a – h – a)
f ’ (a–) = lim (h→0) f(a+h) – f(a) / -h = slope of tangent at A from LHS
f ’ (a–) = Left-hand derivative at x=a
If f ’(a+) = f ’(a–) = a finite quantity, then f(x) is said to be differentiable at x=a; and in this case curve y = f(x) has a unique tangent (Not Shown) of finite slope at x = a.
f ’(a+) = f ’(a–) = f ’(a) = finite slope of the tangent at x = 0.
THEOREM- If a function is differentiable at x=a then it is also continuous at x = a.
NOTE-
- Differentiability ⇒ Continuity
- Continuity ⁄⇒ Differentiability
- Discontinuity ⇒ Non-Differentiability
- Non-Differentiability ⁄⇒ Discontinuity
NOTE- If f ’(a+) = p and f ’(a–) = q where ‘p’ and q” are finite values, then
- If p = q then f(x) is differentiable at x=a and continuous at x = a.
- If p ≠ q then f(x) is not differentiable at x = a, but may or may not be continuous at x = a.
- f(x) is not differentiable but continuous at x=a then the geometrical graph of the function has a sharp corner at x = a. For Example- See graph of f(x) = |x|
- If the graph of the function exhibits a sharp corner at x=a, it means unit tangent can’t be drawn at x = a.
Differentiability in an Interval
- A function is said to be differentiable in (a, b) if it is differentiable at each and every point of the interval.
- Differentiable at [a, b] if
It is differentiable in (a, b) f’ (a+) = limit(h→0) {(f(a+h)- f(a)) / h} = a finite quantity f’ (a–) = limit(h→0) {(f(b-h)- f(a)) /- h} = a finite quantity
- All trigonometric, logarithmic, exponential and polynomial functions are differentiable in their domain (Inverse Trigonometric Functions are not included).
Note-
- Derivative in an interval should be checked at all those points where f(x) may be discontinuous.
- For |f(x)| differentiability should be checked at those points where f(x) = 0.
For Example- Consider a differentiable function f(x) whose graph is given as- Fig.- A
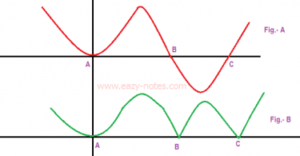
|f(x)| → Fig.- B F(x) = 0 at A, B, C At x= A |f(x)| is derivable; but may or may not be derivable at x = B & C.
Q-> Try to solve these functions?
(i) f(x) = |x3| (ii) f(x) = |x(x-1)|(iii) f(x) = (x-1)|x2 – 3x + 2|
Important Points to Remember
- If f(x) and g(x) both are differentiable function at x = a then f(x) ± g(x), f(x)×g(x) and f(x)/g(x)[g(x)≠0] will also be differentiable at x = a.
- If f(x) differentiable and g(x) is not differentiable at x = a then f(x) ± g(x) will not be differentiable but nothing definite can be said about derivative of function f(x) × g(x) and f(x)/g(x)[where g(x) ≠ 0] at x = a.
- If f(x) and g(x) both are not differentiable at x = a then nothing definite can be said about derivative of function f(x) × g(x) and f(x)/g(x) [where g(x)≠0] at x = a.
- A derivative of a continuous function need not be continuous.
Ex- f(x)= Two cases Case-1 f(x)= x2sin(1/x); x≠0 Case-2 f(x)= 0; x=0
- If f(x) is derivable at x = a and f(a)=0 and g(x) is continuous at x = a then product function f(x)g(x) will also be derivable at x =a.
- If f(x) is differentiable at x = a and p(h) and g(h) approaches to zero as h → 0
limit (h→0) f(a+p(h)) – f(a+ g(h))/ p(h)- g(h) = f’(a)
Determination of functions which are differentiable and satisfying some given functional rule
Four Basic Steps
- Write the expression for f'(x) whether LHD or RHD
f'(x) = limit(h→0) {f(x+h) – f(x)}/ h
- Manipulate f(x+h)-f(x) using functional rule and get f'(x) in its simplifying form.
- Integrate both sides and f(x) with the constant of its integration.
- Using a suitable value of ‘x’, get the value of the constant of integration.
Methods of Differentiation
Symbols used for derivative
dy/dx or f ‘(x) or D(y) or y’ or y1 → First Order Derivative
d2y/dx2 or f ”(x) or D2(y) or y” or y2 → Second Order Derivative
Derivative of some standard Functions
- d(xn)/dx =nxn-1 n ∈ R; x>0
- d(ax)/dx =ax ln a a>0
- d(ex)/dx =ex
- d(ln x)/dx = 1/x
Trigonometric Functions
- d(sin x)/dx = cos x
- d(cos x)/dx = -sin x
- d(sec x)/dx = sec x tan x
- d(cosec x)/dx = -cot x cosec x
- d(tan x)/dx = sec2 x
- d(cot x)/dx = –cosec2 x
Inverse Trigonometric Functions
- d(sin-1x)/dx = 1/(1-x2)1/2 -1< x <1
- d(cos-1x)/dx = -1/(1-x2)1/2 -1< x <1
- d(cot-1x)/dx = -1/(1+x2) x∈ R
- d(tan-1x)/dx = 1/(1+x2) x∈ R
- d(sec-1x)/dx = 1/|x|(x2-1)1/2 |x|>1
- d(cosec-1x)/dx = -1/|x|(x2-1)1/2 |x|>1
Rules in Differentiation
Sum or Difference Rule
If h (x) = f(x) ± g (x)
then h’ (x) = f ‘(x) ± g’ (x)
Constant Multiple Rule
If h (x) = k f(x) where k is any constant h’ (x) = k f ‘(x)
Product Rule
h (x) = f(x) × g (x) then h’ (x) = f ‘(x) g (x) + g’ (x) f(x) Note- (fgh)’ = (fg)h’ + (fh)g’ + (gh)f ‘ or (fhg)’ = {f(gh)’ + g(fh)’ + h(fg)’}/2
Quotient Rule
d{f(x)/g(x)}/dx = {f ‘(x) g (x) + g’ (x) f(x)}/g2(x) Also- d{1/f (x)}/dx = – f ‘(x)/f2(x)
Chain Rule
If y = f(t); t = g(u); u = h(x) then, dy/dx = dy/dt × dt/du × du/dx = f ‘(t) × g'(u) × h'(x)