Short Notes on Vortex Motion
Vortex Motion Definition
- A whirling or rotating mass of fluid is called vortex flow.
- The flow of the fluid in a curved path.
Read Also- Fluid Mechanics: Objective Questions
Free Vortex Flow
In this flow fluid mass rotates due to the conservation of angular momentum. The velocity profile is inversely proportional to the radius.
v × r = constant
The point at the center of rotation is called a singular point, where velocity approaches to infinite. An example of free vortex motion is whirling mass of liquid in a washbasin, whirlpool in the river, etc.
Points to remember:
- No external torque or energy is required.
- In free vortex flow, Bernoulli’s equation can be applied.
Forced Vortex Flow
When a fluid is rotated about a vertical axis at a constant speed, such every particle of it has the same angular velocity, the motion is known as the forced vortex.
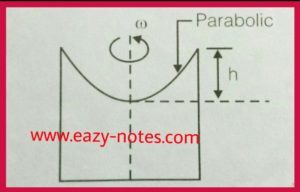
v = r × ω
h = ω²r²/2g
Where ‘h’ is a height of paraboloid, and r is the radius of the cylinder.
The volume of paraboloid = 1/2 π ×r² h
= 1/2 of the volume of circumscribing cylinder
Points to Remember
- The surface profile of a forced vortex flow is parabolic.
- Forced vortex requires a constant supply of external energy or torque.
An example of forced vortex flow is a rotating cylinder and flow inside the centrifugal pump.
Read More- Buoyancy and Floatation Notes
Variation of Pressure
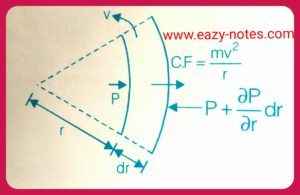
dp = (ρv²/r) × dr – ρg dz
z is in the upward direction
Equation of Free Vortex Flow
We know for free vortex v × r = constant = k
and dp = (ρv²/r) × dr – ρg dz
dp = [{(ρ × k²)/r×r² }× dr] + ρg dz (putting v = k/r)
On Integration for point 1 to point 2
∫dp = ∫[{(ρ×k²)/r³ }× dr] – ρg ∫dz
P2 – P1 = ρ/2 (v1² – v2²) – ρg(z2 – z1) (Again putting value of k )
P1 + ½ ρv1² + ρgz1 = P2 + ½ ρv2² + ρgz2 (Bernoulli’s Equation is applicable in Free Vortex)
Equation of Forced Vortex Flow
We know for free vortex v/r = ω = constant
dp = [(ρ×ω²r²)/r] × dr + ρg dz
On Integration for point 1 to point 2
∫dp = ρ×ω² ∫r × dr + ρg ∫dz
P2 – P1 = ρω²/2 (r2² – r1²) – ρg(z2 – z1)
On Putting v = ω × r
P2 – P1 = ρ/2 (v2² – v1²) – ρg(z2 – z1)
P1 – ½ ρv1² + ρgh1 = P2 – ½ ρv2² + ρgz2 (Bernoulli’s Equation Not Applicable)
Free Vortex and Forced Vortex Flow Differences
Let us look at some of the differences between Free Vortex and Forced Vortex.
| Free Vortex Flow | Forced Vortex Flow |
| No external torque i.e. torque required to rotate is zero. | External torque is required to rotate the fluid mass. |
| We know T = d (mvr)/dt and since T = 0, So, mvr = constant or v × r = constant (mass is constant) | ω = constant v/r = constant |
Read More- Material Science Objective Questions